Intérêts composés (intérêt cumulé)
Dernière mise à jour : 2 février 2023
L’intérêt composé (intérêt sur intérêt) est un principe extrêmement puissant qui garantit que vous pouvez devenir très prospère en investissant.
Ce n’est pas un concept avec lequel vous avez une chance de devenir riche rapidement, mais un concept où vous pouvez être assuré de devenir riche à long terme.
Si vous souhaitez gagner de l’argent grâce aux intérêts composés le plus rapidement possible, je peux vous conseiller d’investir dans des ETF ou des actions via le courtier à bas prix DEGIRO.
1. Qu'est-ce que l'intérêt composé?
L’intérêt composé est simplement le principe de gagner des intérêts sur vos intérêts.
Le concept repose sur ces faits :
- Chaque année que vous investissez, votre investissement augmente d’un certain pourcentage (l’intérêt/le rendement).
L’année suivante, les intérêts des années précédentes porteront également intérêt – à condition qu’un intérêt composé leur soit appliqué. Ce n’est pas toujours le cas.
Juste un exemple rapide, avec un investissement initial de 1000 € et un rendement annuel de 10%:
- Année 1: Votre investissement augmente de 10%, votre rendement est de 100 €, donc votre capital total en fin d’année est de 1100 €
- Année 2: Vous obtenez un autre rendement de 10%, mais cette fois, c’est sur les 1100 €. Votre retour est donc de 110 €, ce qui porte votre capital à 1210 €. Vous obtenez donc 10 € de plus simplement parce que vous avez également perçu des intérêts sur vos intérêts.
- Année 3: le rendement de 10% de 1210 € est de 121 €, ce qui signifie que votre capital passera à 1331 €.
Et ainsi de suit, chaque année après cela, votre capital augmentera de plus en plus vite.
Comme vous pouvez le voir, avec un tel rendement, vous doublerez rapidement votre capital.
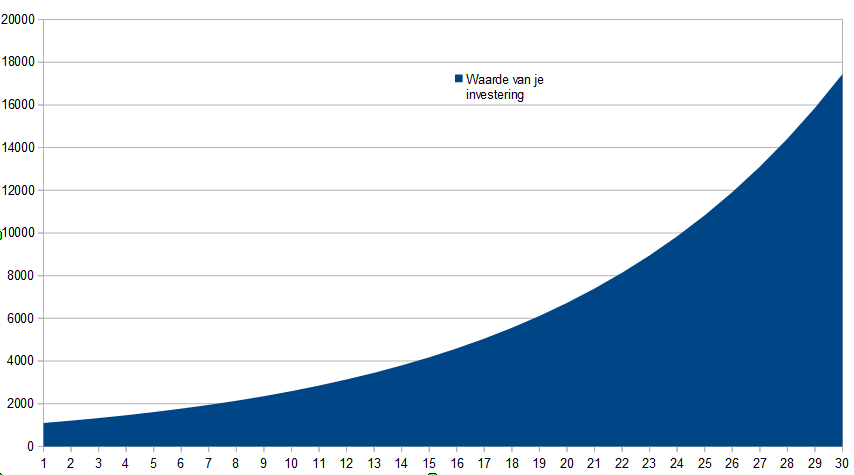
Après dix ans, vous auriez 2594 €, après 20 ans 6727 € et après 30 ans 17 449 €.
Votre investissement initial a été de x17 en trente ans.
Cela ne semble pas très impressionnant, en 30 ans vous n’avez que 17 000 €… mais rappelez-vous que c’était avec un investissement modeste de 1 000 €.
Imaginez que vous investissiez 50 000 € et receviez des intérêts sur les intérêts pendant 30 ans, puis vous aurez un joli 850 000 € à la fin de ce trajet.
C’est le pouvoir de l’intérêt sur l’intérêt.
Vous pouvez le calculer vous-même via un document Excel ou via Airtable, mais il existe également des calculateurs d’intérêts composés gratuits en ligne.
2. La règle de 72
Une règle empirique que vous pouvez utiliser pour estimer à quelle vitesse votre argent augmentera avec les intérêts composés est la règle de 72:
Divisez 72 par votre numéro en pourcentage d’intérêt et vous obtenez le nombre d’années qu’il faut pour doubler votre argent.
Dans notre exemple, c’est 72/10 = 7,2. Après un peu plus de 7 ans, vos 1000 € valent environ 2000 €.
Ce principe est la principale raison pour laquelle vous devriez commencer à investir dès que possible.
Plus vous commencez tôt, plus vous pouvez faire l’expérience de cycles de doublement dans votre vie.
Si vous commencez à investir à 20 ans et que vous avez un cycle de doublement d’environ 10 ans, votre investissement vaudra quatre fois plus à 60 ans qu’une personne qui ne commence à investir qu’à 40 ans:
- A vingt ans, vous investissez 1000 € et vous n’en faites plus. Après 10 ans, à trente ans, vous avez 2000 €. 4000 € à 40 ans et 16000 € à 60 ans.
- Quelqu’un qui ne commence qu’à 40 ans ne pourra faire fructifier que 1000 € à 4000 € avant d’avoir 60 ans.
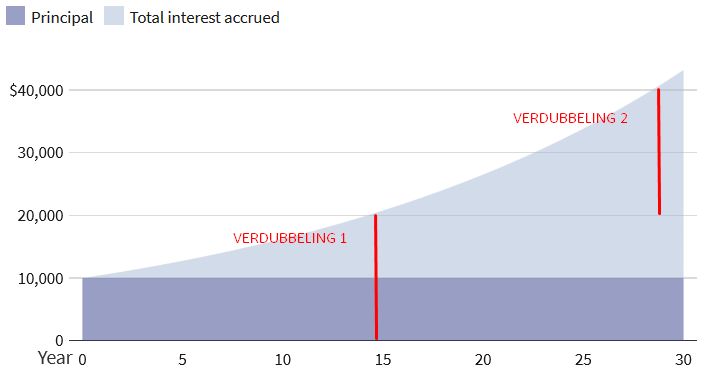
Le graphique ci-dessous d’Investopedia montre bien les périodes de doublement.
On voit ici une somme initiale de 10 000 $ avec un rendement de 5%.
72 divisé par 5 est un peu moins de 15, donc sur une période de 30 ans, vous prévoyez 2 périodes de doublement.
Après 15 ans, les 10 000 $ ont doublé à 20 000 $, pour doubler à nouveau à 40 000 $ 15 ans plus tard.
Encore deux choses avant de continuer. Dans les exemples ci-dessus:
- Pour faire simple, nous avons seulement supposé une somme initiale. Mais si vous déposez fréquemment de l’argent supplémentaire, même s’il s’agit de petites sommes, vous commencerez à recevoir beaucoup plus d’intérêts sur les intérêts – selon la fréquence à laquelle l’intérêt composé sera calculé.
- Nous avons utilisé une année comme période au cours de laquelle le taux d’intérêt est recalculé. Mais plus vous avez une telle période fréquemment, plus vous recevrez d’intérêt pour votre intérêt. Ainsi, si votre intérêt est calculé quotidiennement, vous avez constamment un effet d’intérêt compensé. Cela peut être le cas de certains comptes d’épargne.
3. Intérêt simple et composé
L’intérêt composé, ou l’intérêt cumulé, est le contraire de l’intérêt simple.
Avec un simple intérêt, vous n’obtenez des intérêts que sur votre investissement initial. L’intérêt que vous recevez reste donc le même, quelle que soit la durée de votre épargne.
Dans l’exemple ci-dessus, vos 1000 € gagneront 100 € chaque année, s’il y a un intérêt simple.
En 30 ans, vous pouvez augmenter votre somme initiale à 4000 € (1000 € + 30 * 100 €).
Pas mal en soi, mais comparé à x17 avec intérêt composé, il est carrément bas.
Les obligations suivent généralement le principe de l’intérêt simple.
Vous recevrez un coupon basé sur votre montant principal chaque année pendant la durée de vie de l’obligation.
Cela fait des obligations un investissement sûr: vous savez ce que vous gagnerez chaque année, et après l’échéance, vous récupérez votre investissement initial.
La maxime « plus il y a de risque, plus il y a de rendement » s’applique souvent à l’inverse: « moins il y a de risque, moins il y a de rendement ».
4. Exemples d'intérêt composé / intérêt cumulé
4.1 Intérêts composés sur un compte d'épargne
C’est la forme la plus courante d’intérêt composé, et la plupart des gens en ont l’expérience.
Vous recevez un certain pourcentage d’intérêt de base sur votre compte d’épargne.
Ce montant est généralement calculé quotidiennement et est payé une fois par an.
En plus du taux de base, vous avez souvent également une prime de fidélité, où vous recevez de l’argent supplémentaire si vous ne touchez pas à votre argent pendant une certaine période.
Comme je l’ai déjà indiqué dans plusieurs articles, les taux d’intérêt dans les banques sont extrêmement bas ces jours-ci (<1%) et on ne peut même pas éviter l’inflation.
L’inflation est un problème très sérieux à long terme.
Beaucoup de gens n’en sont pas conscients et pensent qu’économiser de l’argent à long terme est toujours une bonne idée.
Si vous mettez simplement votre argent dans un compte d’épargne, il perdra de la valeur chaque année et même avec des intérêts composés, il faudra beaucoup de temps pour réaliser un profit.
A titre d’illustration: si vous avez 1000 € sur votre compte épargne et que vous gagnez 0,50% d’intérêts, après trente ans vous aurez 1161 €.
La période de doublement est de 144 ans.
A éviter, vous ne deviendrez pas riche aussi vite !
4.2 Intérêt composé en bourse
L’intérêt composé en investissant en bourse fonctionne différemment du modèle standard d’intérêt cumulé, comme sur un compte d’épargne.
En bourse, vous faites en moyenne 8% de profit par an, mais ce n’est pas la même chose que les intérêts.
Après tout, l’intérêt est quelque chose que vous recevez réellement, mais le profit de la bourse est exprimé en actions qui valent plus au fil du temps.
Hors dividendes (voir section suivante), vous ne recevrez pas d’argent périodiquement pour vos investissements en bourse.
La valeur des intérêts composés en bourse s’exprime donc davantage dans la valeur totale de vos actions sur une longue période.
En bref:
- Vous achetez quelques actions qui valent 100% de leur valeur la première année.
- Dans leur deuxième année, ils valent 108%
- Dans leur troisième année, ils augmentent encore 8%, donc ils valent (108 + 8,64 =) 116,64%.
- La quatrième année, ils valent (116,64 + 9,3312 =) 125,9712
- Après dix ans, vos actions vont valoir 200% de leur valeur d’origine, après 20 ans plus de 400% et après 30 ans plus de 900%.
Dans l’ensemble, une forme d’investissement très intéressante, surtout si l’on considère que la section suivante est ajoutée à ceci:
4.3 Intérêts composés avec dividendes
Un dividende est une somme d’argent spécifique que vous recevez pour chaque action que vous détenez d’une société de distribution de dividendes.
J’ai discuté de cela plus en détail dans Qu’est ce qu’un dividende?.
Le principe de l’intérêt composé en ce qui concerne les dividendes se résume à réinvestir les paiements de vos dividendes pour acheter plus d’actions qui paieront vos dividendes.
Au fil du temps, vous pourrez acheter plus d’actions avec vos revenus de dividendes qu’avec votre investissement mensuel dans les actions.
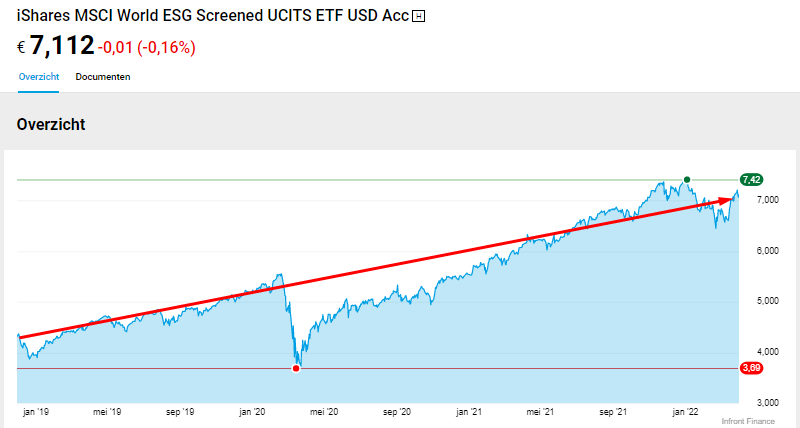
L’exemple ci-dessous utilise les chiffres réels d’un ETF (Exchange-Traded Fund, FNB) existant pour démontrer comment les intérêts composés fonctionnent avec les dividendes et la force de ce principe.
Surtout lorsque vous considérez que vous devez le combiner avec la croissance des intérêts composés du ETF lui-même, comme indiqué dans la section précédente.
4.3.1 Prémisse
Pour cet exemple, je vais prendre un ETF qui coûte 24 € avec un dividende de 1,22 € par an.
J’achète cet ETF deux fois par mois, pour un investissement total de 48 € par mois et 576 € par an (24 € * 2 * 12).
Je réinvestis l’argent que je gagne grâce aux dividendes dans l’ETF.
4.3.2 Résultat
- Après dix ans, mon propre investissement serait de 5760 € (24 € * 2 * 12 * 10).
Grâce aux dividendes supplémentaires que j’ai pu acheter, mes actions dans ce ETF/FNB valent 7273 € (investissement propre + valeur des actions supplémentaires achetées avec les dividendes gagnés), donc j’ai 1513 € de profit (l’augmentation attendue de 8% par an dans le ETF non inclus).
À ce stade, je gagne environ 370 € par année grâce à mes dividendes.
- Après vingt ans, mon propre investissement est de 11.520 €, les actions valent 19.214 € et j’ai un bénéfice de 7694 €. Je gagne environ 976 € par an grâce à mes dividendes.
- Après trente ans, le montant total de l’investissement propre est de 17.280 €, mais les actions valent 38.642 € et mon bénéfice est de 21.362 €. Je gagne près de 2000 € par an grâce à mes dividendes.
La valeur totale de mes actions dans ce FNB est plus du double de celle de mon propre investissement.
Le profit que j’ai réalisé en investissant simplement 48 € par mois est supérieur à vingt mille euros.
Chaque année, je reçois environ 2000 € simplement parce que je suis propriétaire de ces actions.
Et après cela, il ne cesse de monter de plus en plus haut.
Trente ans peuvent sembler longs, mais vous ne pouvez pas vous attendre à devenir riche en quelques années en investissant 40 $ par mois.
Et si vous commencez assez tôt, investir trente ans est tout à fait faisable.
Même quarante à cinquante ans ne posent aucun problème si vous commencez à investir dès que vous commencez à travailler.
Saviez-vous, par exemple, que Warren Buffett, l’une des personnes les plus riches du monde, a fait 90% de sa fortune au cours des dernières années de sa vie, grâce au concept d’intérêt composé qui, après plusieurs décennies d’investissement , est devenu si puissant qu’il a commencé à se multiplier par milliards ?
Même avec un investissement mensuel modéré, n’importe qui peut devenir prospère si vous vous y tenez assez longtemps et régulièrement.
4.3.3 Escalade
Supposons maintenant que vous investissiez 96 € par mois. Encore assez bas, et faisable pour la plupart des gens.
- Après dix ans, vous avez un bénéfice de 3000 €, après vingt ans 15.000 € et après trente ans 43.000 €.
Notez que c’est PROFIT, donc vos actions totales valent 77.600 €!
Supposons maintenant un investissement mensuel de 240 €.
Pouvez-vous deviner la valeur de votre tirelire après quelques décennies?
- Après trente ans, votre propre investissement s’élève à 86.400 € (240 * 12 * 30) et vos investissements valent 193.210 €, ce qui équivaut à plus de 100.000 € de bénéfice et à un dividende annuel d’un peu moins de 10.000 €.
Pas mal!
4.3.4 Retraite
Pour illustrer cela davantage, regardons combien vous devez investir mensuellement pour pouvoir prendre votre retraite après trente ans de revenus d’environ 2000 € par mois de dividendes (24.000 € par an).
Si vous mettez 576 € de côté chaque mois pendant 30 ans, vous aurez économisé un peu plus de 200.000 €, mais vos actions valent un peu moins d’un demi-million, vous réalisez donc un bénéfice de plus de 250.000 €.
Et vous gagnez passivement 1964 € chaque mois.
Si vous voulez être millionnaire en investissant dans cet ETF, vous pouvez y parvenir en investissant 1200 € chaque mois.
Après trente ans, vos investissements valent un peu moins d’un million d’euros, vous réalisez un bénéfice de plus d’un demi-million et vous recevez plus de 4000 € par mois de vos dividendes pour vivre.
Tout cela suppose que la valeur de l’ETF n’augmentera pas au cours de ces trente années (historiquement, c’est le cas, à 8% par an), et que le dividende restera le même (cela peut également augmenter).
Comme il ressort de la section précédente, ces 8% par an auront également un impact énorme.
5. Intérêts composés (intérêt cumulé) résumé
L’intérêt composé est le principe financier extrêmement puissant qui consiste à gagner des intérêts sur vos intérêts.
Votre investissement croît de façon exponentielle à mesure que vous commencez à gagner de plus en plus d’intérêts chaque année.
À court terme, c’est négligeable, mais si vous investissez pendant quelques décennies, vous pouvez facilement voir votre argent multiplié plusieurs fois.
Comme je l’ai montré, vous ne devez pas investir des sommes massives.
Même un maigre 48 € par mois vous rapportera plus de vingt mille euros de profit après trente ans.
Vos actions valent alors plus de quarante mille euros… si elles restaient la même en valeur, ce qui n’est pas le cas.
Le marché augmente en valeur de 8% par an en moyenne, ce qui en trente ans correspond à plus ou moins neuf fois plus de valeur.
Veuillez noter que, pour autant que je sache, les chiffres que j’ai soumis sont corrects, mais il est toujours possible que j’aie fait une erreur quelque part dans mon document Excel.
Ne voyez donc pas cela comme la vérité absolue, mais plutôt comme une illustration du concept, car je peux dire avec une certitude à 100% qu’il est correct.
La leçon à retenir est la suivante: commencez à investir dès que possible.
- Chaque année que vous attendez est perdue.
- Chaque année que vous investissez, vous pouvez prendre votre retraite de plus en plus tôt et vivre de vos investissements.
Intérêt composé + temps = richesse et l’indépendance financière.
J’investis moi-même avec DEGIRO pour plusieurs raisons. Vous pouvez vous inscrire immédiatement et gratuitement via ce lien, vous recevrez même 20 € de crédit de transaction!
Si vous ne savez pas par où commencer, vous pouvez lire mon guide sur la façon d’investir avec DEGIRO en 5 étapes.